The
travelling salesman problem (
TSP) is a problem in
discrete or
combinatorial optimization. It is a prominent illustration of a class of problems in
computational complexity theory which are classified as
NP-hard. Mathematical problems related to the travelling salesman problem were treated in the 1800s by the Irish mathematician Sir
William Rowan Hamilton and by the British mathematician
Thomas Penyngton Kirkman. A discussion of the early work of Hamilton and Kirkman can be found in
Graph Theory 1736-1936.
Problem statement An equivalent formulation in terms of
graph theory is: Given a
complete weighted graph (where the vertices would represent the cities, the edges would represent the roads, and the weights would be the cost or distance of that road), find a
Hamiltonian cycle with the least weight. It can be shown that the requirement of returning to the starting city does not change the
computational complexity of the problem. demonstrated that the generalised travelling salesman problem can be transformed into a standard travelling salesman problem with the same number of cities, but a modified distance matrix.
Computational complexity The problem has been shown to be
NP-hard (more precisely, it is complete for the
complexity class FP; see the
function problem article), and the
decision problem version ("given the costs and a number
x, decide whether there is a roundtrip route cheaper than
x") is
NP-complete. The
bottleneck travelling salesman problem is also NP-hard. The problem remains NP-hard even for the case when the cities are in the plane with
Euclidean distances, as well as in a number of other restrictive cases. Removing the condition of visiting each city "only once" does not remove the NP-hardness, since it is easily seen that in the planar case an optimal tour visits cities only once (otherwise, by the
triangle inequality, a shortcut that skips a repeated visit would decrease the tour length).
 NP-hardness
NP-hardness The traditional lines of attack for the NP-hard problems are the following:
For benchmarking of TSP algorithms,
TSPLIB a library of sample instances of the TSP and related problems is maintained, see the TSPLIB external reference. Many of them are lists of actual cities and layouts of actual
printed circuits.
Devising algorithms for finding exact solutions (they will work reasonably fast only for relatively small problem sizes).
Devising "suboptimal" or
heuristic algorithms, i.e., algorithms that deliver either seemingly or probably good solutions, but which could not be proved to be optimal.
Finding special cases for the problem ("subproblems") for which either better or exact heuristics are possible.
Algorithms An exact solution for 15,112 German towns from TSPLIB was found in 2001 using the
cutting-plane method proposed by
George Dantzig,
Ray Fulkerson, and
Selmer Johnson in
1954, based on
linear programming. The computations were performed on a network of 110 processors located at
Rice University and
Princeton University (see the Princeton external link). The total computation time was equivalent to 22.6 years on a single 500 MHz
Alpha processor. In May 2004, the travelling salesman problem of visiting all 24,978 towns in Sweden was solved: a tour of length approximately 72,500 kilometers was found and it was proven that no shorter tour exists..
Exact algorithms Various
approximation algorithms, which quickly yield good solutions with high probability, have been devised. Modern methods can find solutions for extremely large problems (millions of cities) within a reasonable time which are with a high probability just 2-3% away from the optimal solution.
Several categories of heuristics are recognized.
Heuristics The
nearest neighbour (NN) algorithm lets the salesman start from any one city and choose the nearest city not visited yet to be his next visit. This algorithm quickly yields an effectively short route. Rosenkrantz et al. [1977] showed that the NN algorithm has the approximation factor
Θ(log | V | ). In 2D Euclidean TSP, NN algorithm result in a length about 1.26*(optimal length). Unfortunately, there exist some examples for which this algorithm gives a highly
inefficient route. A bad result is due to the
greedy nature of this algorithm.
Constructive heuristics Pairwise exchange, or
Lin-Kernighan heuristics. The pairwise exchange or '2-opt' technique involves iteratively removing two edges and replacing these with two different edges that reconnect the fragments created by edge removal into a new and more optimal tour. This is a special case of the k-opt method. Note that the label 'Lin-Kernighan' is an oft heard misnomer for 2-opt. Lin-Kernighan is actually a more general method.
k-opt heuristic: Take a given tour and delete
k mutually disjoint edges. Reassemble the remaining fragments into a tour, leaving no disjoint subtours (that is, don't connect a fragment's endpoints together). This in effect simplifies the TSP under consideration into a much simpler problem. Each fragment endpoint can be connected to 2
k − 2 other possibilities: of 2
k total fragment endpoints available, the two endpoints of the fragment under consideration are disallowed. Such a constrained 2
k-city TSP can then be solved with brute force methods to find the least-cost recombination of the original fragments. The k-opt technique is a special case of the V-opt or variable-opt technique. The most popular of the k-opt methods are 3-opt, and these were introduced by Shen Lin of Bell Labs in 1965. There is a special case of 3-opt where the edges are not disjoint (two of the edges are adjacent to one another). In practice, it is often possible to achieve substantial improvement over 2-opt without the combinatorial cost of the general 3-opt by restricting the 3-changes to this special subset where two of the removed edges are adjacent. This so called two-and-a-half-opt typically falls roughly midway between 2-opt and 3-opt both in terms of the quality of tours achieved and the time required to achieve those tours.
V'-opt heuristic: The variable-opt method is related to, and a generalization of the k-opt method. Whereas the k-opt methods remove a fixed number (k) of edges from the original tour, the variable-opt methods do not fix the size of the edge set to remove. Instead they grow the set as the search process continues. The best known method in this family is the Lin-Kernighan method (mentioned above as a misnomer for 2-opt). Shen Lin and Brian Kernighan first published their method in 1972, and it was the most reliable heuristic for solving travelling salesman problems for nearly two decades. More advanced variable-opt methods were developed at Bell Labs in the late 1980s by David Johnson and his research team. These methods (sometimes called Lin-Kernighan-Johnson) build on the Lin-Kernighan method, adding ideas from tabu search and evolutionary computing. The basic Lin-Kernighan technique gives results that are guaranteed to be at least 3-opt. The Lin-Kernighan-Johnson methods compute a Lin-Kernighan tour, and then perturb the tour by what has been described as a mutation that removes at least four edges and reconnecting the tour in a different way, then v-opting the new tour. The mutation is often enough to move the tour from the local well identified by Lin-Kernighan. V-opt methods are widely considered the most powerful heuristics for the problem, and are able to address special cases, such as the Hamilton Cycle Problem and other non-metric TSPs that other heuristics fail on. For many years Lin-Kernighan-Johnson had identified optimal solutions for all TSPs where an optimal solution was known and had identified the best known solutions for all other TSPs on which the method had been tried.
Iterative improvement TSP is a touchstone for many general heuristics devised for combinatorial optimisation such as
genetic algorithms,
simulated annealing,
Tabu search, and
ant colony optimization.
Optimised
Markov chain algorithms which utilise local searching heuristic sub-algorithms can find a route extremely close to the optimal route for 700 to 800 cities.
Random path change algorithms are currently the state-of-the-art search algorithms and work up to 100,000 cities. The concept is quite simple: Choose a random path, choose four nearby points, swap their ways to create a new random path, while in parallel decreasing the upper bound of the path length. If repeated until a certain number of trials of random path changes fail due to the upper bound, one has found a local minimum with high probability, and further it is a global minimum with high probability (where high means that the rest probability decreases exponentially in the size of the problem - thus for 10,000 or more nodes, the chances of failure is negligible).
Randomised improvement Suppose that the number of towns is = 60. For a random search process, this is like having a deck of cards numbered 1, 2, 3, ... 59, 60 where the number of permutations is of the same order of magnitude as the total number of atoms in the known universe. If the hometown is not counted the number of possible tours becomes 60*59*58*...*4*3 (about 10. See also Goldberg, 1989.
Example letting the inversion operator find a good solution Artificial intelligence researcher
Marco Dorigo described in 1997 a method of heuristically generating "good solutions" to the TSP using a simulation of an ant colony called
ACS.
ACS sends out a large number of virtual ant agents to explore many possible routes on the map. Each ant probabilistically chooses the next city to visit based on a heuristic combining the distance to the city and the amount of virtual pheromone deposited on the edge to the city. The ants explore, depositing pheromone on each edge that they cross, until they have all completed a tour. At this point the ant which completed the shortest tour deposits virtual pheromone along its complete tour route (
global trail updating). The amount of pheromone deposited is inversely proportional to the tour length; the shorter the tour, the more it deposits.
After a sufficient number of rounds, the shortest tour found will be, heuristically, close to the optimum length. According to Dorigo, "ACS finds results which are at least as good as, and often better than, those found by the other methods," particularly on asymmetric instances, but this referred only to methods already known at that time.
Ant colony optimization Special cases A very natural restriction of the TSP is the
triangle inequality. That is, for any 3 cities A, B and C, the distance between A and C must be at most the distance from A to B plus the distance from B to C. Most natural instances of TSP satisfy this constraint.
In this case, there is a
constant-factor approximation algorithm (due to Christofides, 1975) which always finds a tour of length at most 1.5 times the shortest tour. In the next paragraphs, we explain a weaker (but simpler) algorithm which finds a tour of length at most twice the shortest tour.
The length of the
minimum spanning tree of the network is a natural lower bound for the length of the optimal route. In the TSP with
triangle inequality case it is possible to prove upper bounds in terms of the
minimum spanning tree and design an algorithm that has a provable upper bound on the length of the route. The first published (and the simplest) example follows.
It is easy to prove that the last step works. Moreover, thanks to the triangle inequality, each skipping at Step 4 is in fact a shortcut, i.e., the length of the cycle does not increase. Hence it gives us a TSP tour no more than twice as long as the optimal one.
The Christofides algorithm follows a similar outline but combines the minimum spanning tree with a solution of another problem, minimum-weight
perfect matching. This gives a TSP tour which is at most 1.5 times the optimal. It is a long-standing (since 1975) open problem to improve 1.5 to a smaller constant. It is known, however, that there is no polynomial time algorithm that finds a tour of length at most 1/219 more than optimal, unless
P =
NP (Papadimitriou and Vempala, 2000). In the case of the bounded metrics it is known that there is no polynomial time algorithm that constructs a tour of length at most 1/388 more than optimal, unless
P =
NP (Engebretsen and Karpinski, 2001). The best known polynomial time approximation algorithm for the TSP problem with distances
one and
two finds a tour of length at most 1/7 more than optimal (Berman and Karpinski, 2006).
The Christofides algorithm was one of the first
approximation algorithms, and was in part responsible for drawing attention to approximation algorithms as a practical approach to intractable problems. As a matter of fact, the term "algorithm" was not commonly extended to approximation algorithms until later. At the time of publication, the Christofides algorithm was referred to as the Christofides heuristic.
Construct the
minimum spanning tree.
Duplicate all its edges. That is, wherever there is an edge from
u to
v, add a second edge from
u to
v. This gives us an
Eulerian graph.
Find a
Eulerian cycle in it. Clearly, its length is twice the length of the tree.
Convert the Eulerian cycle into the
Hamiltonian one in the following way: walk along the Eulerian cycle, and each time you are about to come into an already visited vertex, skip it and try to go to the next one (along the Eulerian cycle).
Triangle inequality and the Christofides algorithm Euclidean TSP, or
planar TSP, is the TSP with the distance being the ordinary
Euclidean distance. Although the problem still remains NP-hard, it is known that there exists a subexponential time algorithm for it. Moreover, many heuristics work better.
Euclidean TSP is a particular case of TSP with triangle inequality, since distances in plane obey triangle inequality. However, it seems to be easier than general TSP with triangle inequality. For example, the minimum spanning tree of the graph associated with an instance of Euclidean TSP is a
Euclidean minimum spanning tree, and so can be computed in expected O(
n log
n) time for
n points (considerably less than the number of edges). This enables the simple 2-approximation algorithm for TSP with triangle inequality above to operate more quickly.
In general, for any
c > 0, there is a polynomial-time algorithm that finds a tour of length at most (1 + 1/
c) times the optimal for geometric instances of TSP in O(
cn log
n) time; this is called a
polynomial-time approximation scheme and is due to
Sanjeev Arora. In practice, heuristics with weaker guarantees continue to be used.
Euclidean TSP In most cases, the distance between two nodes in the TSP network is the same in both directions. The case where the distance from A to B is not equal to the distance from B to A is called asymmetric TSP. A practical application of an asymmetric TSP is route optimisation using street-level routing (asymmetric due to one-way streets, slip-roads and motorways).
Asymmetric TSP Solving an asymmetric TSP graph can be somewhat complex. The following is a 3x3 matrix containing all possible path weights between the nodes A, B and C. One option is to turn an asymmetric matrix of size N into a
symmetric matrix of size 2N, doubling the complexity.
To double the size, each of the nodes in the graph is duplicated, creating a second
ghost node. Using duplicate points with very low weights, such as -∞, provides a cheap route "linking" back to the real node and allowing symmetric evaluation to continue. The original 3x3 matrix shown above is visible in the bottom left and the inverse of the original in the top-right. Both copies of the matrix have had their diagonals replaced by the low-cost hop paths, represented by -∞.
The original 3x3 matrix would produce two Hamiltonian cycles (a path that visits every node once), namely A-B-C-A [score 12] and A-C-B-A [score 9]. Evaluating the 6x6 symmetric version of the same problem now produces many paths, including A-A'-B-B'-C-C'-A, A-B'-C-A'-A, A-A'-B-C'-A [all score 9-∞].
The important thing about each new sequence is that there will be an alternation between dashed (A',B',C') and un-dashed nodes (A,B,C) and that the link to "jump" between any related pair (A-A') is effectively free. A version of the algorithm could use any weight for the A-A' path, as long as that weight is
lower than all other path weights present in the graph. As the path weight to "jump" must effectively be "free", the value zero (0) could be used to represent this cost— if zero is not being used for another purpose already (such as designating invalid paths). In the two examples above, non-existent paths between nodes are shown as a blank square.
 Solving by conversion to Symmetric TSP
Solving by conversion to Symmetric TSP The TSP, in particular the
Euclidean variant of the problem, has attracted the attention of researchers in
cognitive psychology. It is observed that humans are able to produce good quality solutions quickly. The first issue of the
Journal of Problem Solving is devoted to the topic of human performance on TSP.
Human performance on TSP Many quick algorithms yield approximate TSP solution for large city number. To have an idea of the precision of an approximation, one should measure the resulted path length and compare it to the exact path length. To find out the exact path length, there are 3 approaches:
find a lower bound of it,
find an upper bound of it with CPU time T, do extrapolation on T to infinity so result in a reasonable guess of the exact value, or
solve the exact value without solving the city sequence.
TSP path length Consider N points are randomly distributed in one unit square, with N>>1. A simple lower bound of the shortest path length is

, obtained by considering each point connects to its nearest neighbor which is

distance away on average.
Another lower bound is
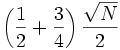
, obtained by considering each point j connects to j's nearest neighbor, and j's second nearest neighbor connects to j. Since j's nearest neighbor is (1/2)/sqrt(N) distance away; j's second nearest neighbor is (3/4)/sqrt(N) distance away on average.
David S. Johnson had got a lower bound by experiment
Christine L. Valenzuela and Antonia J. Jones have also explored a better lower bound by experiment
Lower bound The board game
Elfenland resembles the travelling salesman problem.
Notes D. L. Applegate, R. E. Bixby, V. Chvátal and W. J. Cook (2006). The Traveling Salesman Problem: A Computational Study. Princeton University Press. ISBN 978-0-691-12993-8. E. L. Lawler and Jan Karel Lenstra and A. H. G. Rinnooy Kan and D. B. Shmoys (1985). The Traveling Salesman Problem: A Guided Tour of Combinatorial Optimization. John Wiley & Sons. ISBN 0-471-90413-9. G. Gutin and A. P. Punnen (2006). The Traveling Salesman Problem and Its Variations. Springer. ISBN 0-387-44459-9. G. B. Dantzig, R. Fulkerson, and S. M. Johnson,
Solution of a large-scale traveling salesman problem, Operations Research 2 (1954), pp. 393-410.
S. Arora. "
Polynomial Time Approximation Schemes for Euclidean Traveling Salesman and other Geometric Problems". Journal of ACM, 45 (1998), pp. 753-782.
P. Berman,
M. Karpinski, "
8/7-Approximation Algorithm for (1,2)-TSP", Proc. 17th ACM-SIAM SODA (2006), pp. 641-648.
N. Christofides,
Worst-case analysis of a new heuristic for the travelling salesman problem, Report 388,
Graduate School of Industrial Administration, Carnegie Mellon University, 1976.
L. Engebretsen,
M. Karpinski,
Approximation hardness of TSP with bounded metrics, Proceedings of 28th ICALP (2001), LNCS 2076, Springer 2001, pp. 201-212.
J. Mitchell. "
Guillotine subdivisions approximate polygonal subdivisions: A simple polynomial-time approximation scheme for geometric TSP, k-MST, and related problems", SIAM Journal on Computing, 28 (1999), pp. 1298–1309.
S. Rao, W. Smith.
Approximating geometrical graphs via 'spanners' and 'banyans'. Proc. 30th Annual ACM Symposium on Theory of Computing, 1998, pp. 540-550.
C. H. Papadimitriou and Santosh Vempala, "
On the approximability of the traveling salesman problem",
Proceedings of the 32nd Annual ACM Symposium on Theory of Computing, 2000.
Daniel J. Rosenkrantz and Richard E. Stearns and Phlip M. Lewis II (1977). "An Analysis of Several Heuristics for the Traveling Salesman Problem". SIAM J. Comput. 6: 563–581. D. S. Johnson and L. A. McGeoch,
The Traveling Salesman Problem: A Case Study in Local Optimization, Local Search in Combinatorial Optimisation, E. H. L. Aarts and J.K. Lenstra (ed), John Wiley and Sons Ltd, 1997, pp. 215-310.
Thomas H. Cormen,
Charles E. Leiserson,
Ronald L. Rivest, and
Clifford Stein.
Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001.
ISBN 0-262-03293-7. Section 35.2: The traveling-salesman problem, pp. 1027–1033.
Michael R. Garey and David S. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 0-7167-1045-5. A2.3: ND22–24, pp.211–212.
MacGregor, J. N., & Ormerod, T. (1996). Human performance on the traveling salesman problem. Perception & Psychophysics, 58(4), pp. 527–539.
Vickers, D., Butavicius, M., Lee, M., & Medvedev, A. (2001). Human performance on visually presented traveling salesman problems. Psychological Research, 65, pp. 34–45.
William Cook, Daniel Espinoza, Marcos Goycoole (2006). Computing with domino-parity inequalities for the TSP. INFORMS Journal on Computing. Accepted.
Goldberg, D. E. Genetic Algorithms in Search, Optimization & Machine Learning. Addison-Wesley, New York, 1989.




 Selected Filmography
Selected Filmography

 Co-ordination Centre
Co-ordination Centre NP-hardness
NP-hardness Solving by conversion to Symmetric TSP
Solving by conversion to Symmetric TSP , obtained by considering each point connects to its nearest neighbor which is
, obtained by considering each point connects to its nearest neighbor which is  distance away on average.
distance away on average.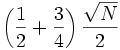 , obtained by considering each point j connects to j's nearest neighbor, and j's second nearest neighbor connects to j. Since j's nearest neighbor is (1/2)/sqrt(N) distance away; j's second nearest neighbor is (3/4)/sqrt(N) distance away on average.
, obtained by considering each point j connects to j's nearest neighbor, and j's second nearest neighbor connects to j. Since j's nearest neighbor is (1/2)/sqrt(N) distance away; j's second nearest neighbor is (3/4)/sqrt(N) distance away on average.
 In popular culture
In popular culture History
History Image search is a kind of
Image search is a kind of  Google
Google





 Cathedral Close
Cathedral Close Lefthit
Lefthit